| France | Cours en ligne | Mathématique Vu 378562 fois
Article N°27579
Mes petits cours de Math. : Système d'équation à deux inconnues
Abordons maintenant les systèmes d’équations à deux inconnues.
Ceux ci vont nous permettre de résoudre des problèmes à deux inconnues. Il nous faudra trouver un couple (x ; y) par exemple qui seront la solution des deux équations.
Il existe plusieurs méthodes :
Nous travaillerons sur un exemple simple de système d’équations.
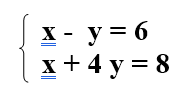
La première méthode est la méthode par substitution :
Elle consiste à isoler une des deux inconnues dans une des équations. Nous choisirons d’isoler x dans la première. Nous plaçons donc notre x d’un côté du égal et le reste de l’autre, ce qui nous donne :
x = y + 6
Nous savons maintenant que "notre" x est égal à (y + 6). Résultat que nous allons substituer à x dans une des deux équations selon notre choix.
Nous choisirons ici de le substituer dans la seconde pour nous apprendre à travailler les deux équations.
( y + 6) + 4 y = 8
5 y = -6 + 8
5 y = 2
y = 2/5
Nous avons trouvé la valeur de y que nous remplaçons dans une de nos deux équations. Prenons par exemple la première :
x - 2/5 = 6
x = 6 + 2/5
x = 30/5 + 2/5 = 32/5
Nous vérifions pour les deux équations en remplaçant les valeurs trouvées pour x et pour y :
32/5 - 2/5 = 30/ 5 = 6 32/5 + 4 X 2/5 = 40/5 = 8
Nos valeurs sont vérifiées exactes et nous pouvons dire que la solution du système d’équation est le couple (2/5 ; 32/5 )
La seconde méthode est la méthode par addition :
Ici nous devons éliminer une des deux inconnues. Reprenons notre système d’équations :
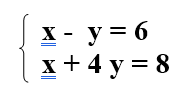
Nous allons donc chercher par quel nombre multiplier nos équations pour pouvoir ensuite les additionner de façon à ce que une de nos inconnues s’annule.
Nous choisissons de multiplier la première par 4.
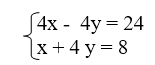
Nous additionnons maintenant nos deux équations :
4x -
Nous continuons à résoudre
5 x = 32
x = 32/5
Nous remplaçons notre x dans une des deux équations et nous trouvons :
32/5 - y = 6
- y = 30/5 - 32/5
- y = - 2/5
y = 2/5
Nous devons vérifier notre résultat. Nous ne le ferons pas ici car nous avons utilisé le même système d’équations et les valeurs trouvées sont les mêmes que par la première méthode.
Notre solution est encore ici le couple : ( 2/5 ; 32/5 )
Résoudre un problème à l'aide d'un système :
Comme pour la mise en équation d’un problème à une inconnue, nous procèderons pas étape pour la mise en système d’équations :
Prenons un exemple :
Un gymnase rectangulaire a un périmètre de 260 m.
La longueur mesure 20 m de plus que la largeur.
Calculez les longueurs et les largeurs de ce gymnase.
Etape 1 : nous définissons nos inconnues. Nous prendre x pour la longueur du gymnase et y pour sa largeur
Etape 2 : nous comprenons les données du problème et les rangeons
Nous avons que
- Que le périmètre du gymnase mesure 260 m.
- Que la longueur mesure 20 mètres de plus que la largueur
Etape 3 : nous analysons les données :
Que le périmètre du gymnase mesure 260 m.
Nous pouvons poser notre première équation :
2x + 2y = 260 (il ne faut pas oublier que le périmètre est égale à :
(LONGUEUR + largeur) X 2
Que la longueur mesure 20 mètres de plus que la largueur
Nous pouvons maintenant poser notre deuxième équation
x = y + 20
Etape 4 : mise en système d’équation du problème
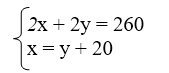
Etape 5 : résolution du système l’équation
Nous choisirons la méthode de substitution car nous avons déjà un x isolé.
2(y + 20) + 2y = 260
2 y + 40 + 2 y = 260
4y = 260 – 40
4 y = 220
y = 55
Nous calculons x :
x = 55 + 20 = 75
Nous vérifions nos résultats dans les deux équations :
(75 X 2) + (55 X 2) = 260 75 = 55 + 20
Notre résultat est juste !
Etape 6 : retranscription du résultat mathématique en réponse littérale :
La longueur du gymnase est égale à 75 m et sa largeur est égale à 55 m.
Notre problème mathématique est résolu.
Etape 6 : retranscription du résultat mathématique en réponse littérale :
La longueur du gymnase est égale à 75 m et sa largeur est égale à 55 m.
Notre problème mathématique est résolu.
Les maths, ce n'est pas si compliqué.
Retrouvez les autres "Petits cours de Math." ici Cliquez ici
Belle journée.
Gaelle Laborie
Réagissez, commentez !
- Aucun commentaire pour l'instant